11259. Минимальная
триангуляция
Вам задан правильный
многоугольник с n вершинами, пронумерованными от 1 до n против часовой стрелки.
Триангуляция данного
многоугольника – это разбиение его на
треугольники, такое что:
·
каждая вершина любого треугольника является вершиной исходного
многоугольника;
·
никакие два треугольника не имеют положительной площади пересечения;
·
площадь объединения всех треугольников равна площади исходного
многоугольника.
Вес триангуляции определяется как
сумма весов входящих в неё треугольников, где вес треугольника равен
произведению меток его вершин.
Найдите минимальный вес среди
всех возможных триангуляций данного многоугольника.
Вход. Одно целое число n (3
≤ n ≤ 500) – количество вершин правильного многоугольника.
Выход. Выведите минимальный вес среди
всех триангуляций заданного многоугольника.
|
Пример
входа 1 |
Пример
выхода 1 |
|
3 |
6 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
4 |
18 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
Рассмотрим
треугольник, который
содержит сторону (1, n). Пусть его третьей вершиной будет x, тогда треугольник имеет
вид (1, n, x).
Если x = n – 1, то мы просто отбрасываем
треугольник (1, n, n – 1), после чего остаётся (n – 1) – угольник, который будем
триангулировать дальше.
Если 1 < x < n – 1, то рассмотрим
треугольник (n,
x, k), где x < k < n.
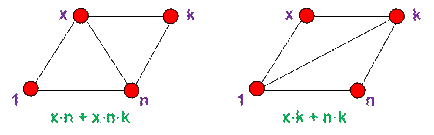
Заменим пару
треугольников (1, x,
n) и (n,
x, k) на пару (1, x, k) и (1, n, k). Суммарный вес треугольников уменьшится, так как xn + xnk > xk
+ nk. После перегруппировки получим
x(n – k) + nk(x – 1) > 0
Неравенство
справедливо, так как n – k > 0 и x – 1 > 0.
Отсюда следует,
что треугольник (1, x,
n) выгоднее заменить на (1, k, n), где k > x. Следовательно, оптимальным выбором будет x = n – 1. Минимальный вес
триангуляции достигается, если провести все диагонали из вершины 1.
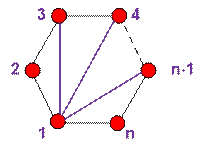
Сумма весов всех треугольников,
исходящих из вершины 1, равна
1 * 2 * 3 + 1 * 3 * 4 + … + 1 * (n – 1) * n = ![]()
Пример
В первом тесте
задан треугольник с вершинами 1, 2, 3. Его вес равен 1 * 2 * 3 = 6.
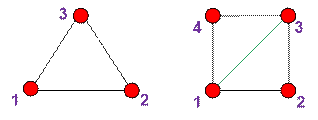
Во втором тесте задан
квадрат с вершинами 1, 2, 3, 4. Минимальный вес достигается при триангуляции с диагональю (1, 3):
1 * 2 * 3 + 1 *
3 * 4 = 6 + 12 = 18
Реализация алгоритма
Читаем входные данные.
scanf("%d", &n);
Вычисляем ответ.
res = 0;
for (i = 2; i < n; i++)
res += 1ll * i * (i + 1);
Выводим ответ.
printf("%lld\n", res);